吉野貴晶のクオンツトピックス

No.20
非ユークリッド距離空間の見える化

2021年12月15日号

投資工学開発部
吉野 貴晶

金融情報誌「日経ヴェリタス」アナリストランキングのクオンツ部門で16年連続で1位を獲得。ビックデータやAI（人工知能）を使った運用モデルの開発から、身の回りの意外なデータを使った経済や株価予測まで、幅広く計量手法を駆使した分析や予測を行う。

投資工学開発部
片山 幸成

ニッセイアセット入社後、デリバティブ取引やファンドのリスク管理業務に従事。18年1月より投資工学開発室にて主に機械学習を含む定量的手法、オルタナティブデータを活用した新たな投資戦略の研究開発を担当。

エキゾチックな距離を直感的に把握してみよう

  • 一風変わった距離のご紹介
  • 非ユークリッド距離空間をどのように表現する？

0. 予備知識、keywords

線形代数の知識を仮定します。

キーワード
距離の定義　超距離　強三角不等式　p進距離　多次元尺度構成法　MDS

1. Introduction

距離というのは、2つの対象が近いか遠いかを定量的に測る指標です。高校数学ではユークリッド距離しか扱いませんが、機械学習ではそれ以外の距離が使われることがあります。例えば、参考文献[ABEJA]ではポワンカレ埋め込みに双曲距離(詳細は[Wiki]参照)が使われています。また、[Qiita]ではp進距離を用いたニューラルネットワークが紹介されています。非ユークリッド距離を用いるメリットとして、[ABEJA]では双曲距離を使うことで、ユークリッド距離より効率的であった事例が紹介されています。一方でデメリットしては、直感的に理解できないという点かと思われます。実際、定義をネットで調べることで計算はできそうですが、どういうものかピンとこないという方が多いのではないでしょうか。今回はそれらの距離空間を見える化する方法をご紹介したいと思います。

2. 抽象的な距離の定義

簡略化のため、2次元平面を前提として議論を進めますが、これは一般の集合上にも拡張できます。距離という概念を私たちは直感的に理解してますが、数学では次のような性質を満たす関数を距離と呼んでいます。一見当たり前な性質ばかりですが、いわゆるコサイン距離は下記の条件を満たしません。

■定義

集合Xの任意の点x , y ,z に対し、非負の関数dが次の性質を満たす時、dをX上の距離と定義します。

  • （1） d（x , y）＝ 0　⇔　x = y.
  • （2） d（x , y）＝ d（y , x）.
  • （3） d（x , z）≦ d（x , y）+ d（y , z）.

また、（3）のより強い条件である（3’）を満たすとき、dをX上の超距離または非アルキメデス的距離と呼びます。

  • （3‘） d（x , z）≦ max{ d（x , y）, d（y , z）}.

（3）を三角不等式、(3’)を強三角不等式と呼びます。

まず（3’）が（3）より強い条件であることを確認します。仮にd（x , y）≦ d（y , z）とすると、（3’）の式はd（x , z）≦ d（y , z）. また、距離関数は非負ですので、0 ≦ d（x , y）. よって、d（x , z）≦ d（y , z）+ d（x , y）. これは（3）式のことでした。d（y , z）≦ d（x , y）の場合も同様です。以上より（3’）が（3）より強い条件であることが確認できました。

ユークリッド距離とp進距離

3. ユークリッド距離

図1

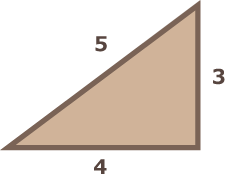
私たちが高校数学等で習った普通の距離を専門的には、ユークリッド距離と呼び、上記の（1）と（2）の性質を持っています。（3）の性質については、例えば余弦定理を思い出せば、上記の性質をもっていることを示すことができます。一方で（4）の性質を持っていないことも明らかなので、ユークリッド距離は超距離（非アルキメデス的距離）ではありません（反例として、例えば図1の高さが3、底辺の長さが4、斜辺の長さが5の直角三角形）。

4. p進距離

次にp進距離について説明します。ここでは、簡単に、整数の場合に限定して定義を述べます（詳細は[Kato]参照)。また、前提として素数pを一つ取って固定されているものとします。

■p進距離の定義

整数a , b に対してp進距離d_pを次で定義する。

  • （p-dist1）a=b の時、d_p（a , b）=0.
  • （p-dist2）a≠b の時、b-a を割り切れるp^n（0≦n, n:整数）の中で、最も大きなnを探して、d_p（a , b）= 1 / p^nとする。

この定義はイデアルadicな位相として一般化できます([Atiyah]参照)。具体的に計算してみましょう。

素数p=3とします。
例えば、a=1、b=28とすると、28-1=27=3^3なので、d_3（1,28）= 1/ 3^3となります。
例えば、a=1、b=11とすると、11-1=10なのでこれは3の倍数でないので、d_3（1,28）=1/ 3^0=1となります。
例えば、a=1、b=16、c=28とすると、d_3（a,c）=1/3^3、d_3（a,b）=1/3、d_3（b,c）=1/3であるから、強三角不等式(3’)が成立していることが分かります。
例えば、a=1、b=16、c=22とすると、d_3（a,c）=1/3、d_3（a,b）=1/3、d_3（b,c）=1/3であるから、強三角不等式（3’）が成立していることが分かります。

5. 分析方法

見える化する方法として、多次元尺度構成法を用います。これは距離行列から適切な配置を計算する方法です。距離行列とは（i, j）成分が地点iと地点j間の距離が入っている行列です。距離の条件（1）から対角成分は常に0で、条件（2）から対称行列になります。
例えば、4点間の距離行列が次のように与えられたとします。
このように与えられたとき、直感的には地点1と2及び地点3と4が各々グループのように配置すればいいわけですが、こういった場合にシステマチックに最適な配置を計算してくれるのが多次元尺度構成法です。

多次元尺度構成法の実行結果

今回はsklearn.manifold.MDS（[MDS]参照）というpythonのライブラリーを使用します。p進距離で計算した場合、各整数がどのような配置になるかを実験してみます。事前にp進距離行列をエクセルで計算して、csvファイルでimportしています。

メインとなるプログラムは、以下の通りです。
mds = manifold.MDS(n_components=2, dissimilarity="precomputed", random_state=1)

  • n_components：
    何次元空間で表現したいか（今回は平面で表したいので2）
  • dissimilarity：
    距離行列が計算済みの場合はprecomputed
  • random_state：
    乱数シードの固定（再現性を担保する必要がある場合は指定、なしでも可）

6. 結果

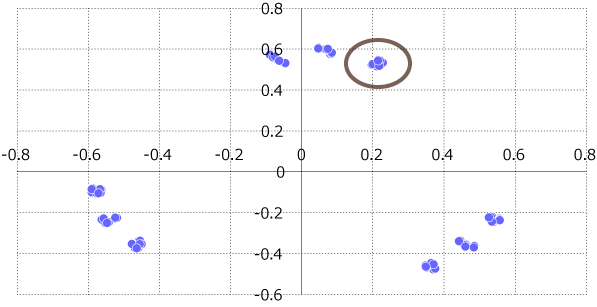
0～99までの整数をp進距離で測って二次元平面に埋め込んだ結果が次の図2です。 左下、右下、上側と大きく三つのグループに分かれた後にその中でさらに、3つのグループに分かれていることが見て取れます。点が密集していて、このままではよく分からないため、上側の〇で囲んだ部分を拡大して見てみましょう。

図2：散布図

結果の解釈と見える化の限界

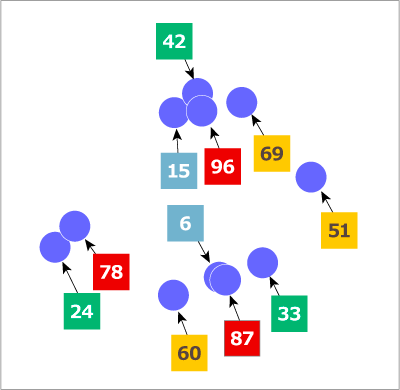
図3では0～24を青色のボックス、25～49を緑色のボックス、50～74を黄色のボックス、75以上を赤色のボックスとしています。

例えば78と24、87と60が非常に近くに配置されていますが、78-24=54=2*3^3、87-60=27=3^3であることからこれはp進距離の定義と整合的であることがわかります。様々な色があることから分かるように数字の大小を比べるユークリッド距離とは全く違う距離であることが直感的に理解できます。

超距離空間においては、開円板の内点が中心になるという直感的には奇妙な性質 ([Kato]参照）があるのですが、さすがにそこまではこの画像からは分からないなど限界もあります。しかし、なんとなくどんな空間か把握したい、雰囲気を知っておきたいというニーズには答えられるのではないでしょうか？

図3

参考文献

吉野貴晶のクオンツトピックス一覧へ

「吉野貴晶のクオンツトピックス」ご利用にあたっての留意点

当資料は、市場環境に関する情報の提供を目的として、ニッセイアセットマネジメントが作成したものであり、特定の有価証券等の勧誘を目的とするものではありません。

【当資料に関する留意点】

  • 当資料は、信頼できると考えられる情報に基づいて作成しておりますが、情報の正確性、完全性を保証するものではありません。
  • 当資料のグラフ・数値等はあくまでも過去の実績であり、将来の投資収益を示唆あるいは保証するものではありません。また税金・手数料等を考慮しておりませんので、実質的な投資成果を示すものではありません。
  • 当資料のいかなる内容も、将来の市場環境の変動等を保証するものではありません。
  • 手数料や報酬等の種類ごとの金額及びその合計額については、具体的な商品を勧誘するものではないので、表示することができません。
  • 投資する有価証券の価格の変動等により損失を生じるおそれがあります。