クオンツトピックス

No.32
深層学習を組み込んだ確率ボラティリティモデル（2）

2025年10月01日号

写真（木村）

ファイナンシャル
テクノロジー運用部
木村 嘉明

ニッセイアセット入社後、リスク管理、国内外株式領域のリサーチ・運用業務等に従事。2025年よりファイナンシャルテクノロジー運用部にて、主に計量的手法・AIを活用したクオンツリサーチおよび投資戦略の開発を担当。

写真（塚本）

ファイナンシャル
テクノロジー運用部
塚本　恵

ニッセイアセット入社後、ファイナンシャルテクノロジー運用部にて主に機械学習を含む数理的な定量的手法、オルタナティブデータを活用した新たな投資戦略の研究開発を担当。

マルコフ連鎖モンテカルロ法を用いてパラメータを推定してみよう

  • 確率ボラティリティモデル＋深層学習モデルの尤度の複雑さについて
  • サンプリングシミュレーションを用いたパラメータ推定について

0. 予備知識、キーワード

基本的な金融工学、深層学習、時系列解析、サンプリングシミュレーションの知識を仮定します。

キーワード
確率ボラティリティモデル、深層学習、マルコフ連鎖モンテカルロ法、シミュレーション

1. イントロダクション

前回記事のNo.31（以下、前回と省略）では、確率ボラティリティモデル（SVモデル）に深層学習を組み込んだStatistical Recurrent Stochastic Volatilityモデル（SR-SVモデル）を紹介しました。このモデルは、SVモデルよりも金融市場における不確実をより柔軟に表せるという特徴があります。応用例として、実際の将来価格データ（実現ボラティリティ）と併せた投資サインの算出や、変動局面に強い資産配分の構築といったものが期待できます。今回は、このモデルのパラメータを実務上どう推定していくかについて紹介します。（通常のSVモデルにも類する部分があります。）

尤度の複雑さとベイズ推定

2. 尤度の複雑さ

前回ご紹介したように、SR-SVモデルは、時系列のリターン\(\{𝑦_𝑡 \}\)に対して以下の式で表されます。

\( h_{t} = SRU((η_{t-1}, z_{t-1}), h_{t-1})　（1） \)
\( η_{t} = β_{0} + β_{1}h_{t} + ξ_{t},　ξ_{t}～N(0,σ^{2})i.i.d.　（2） \)
\( z_{t} = η_{t} + \phi{z_{t-1}}　（3） \)
\( y_{t} = \exp\left( \frac{Z_{t}}{2} \right)ε_{t},　ε_{t}～N(0,1)i.i.d.　（4） \)

ただし、式（1）のSRU構造とは、移動平均と深層学習（リカレントニューラルネットワーク）を組み合わせたものです。（ここで、\(𝛼\)は固定パラメータとします。）

\( r_{t} = \psi (w_{h}h_{t-1}+b_{r})　（5） \)
\( \phi_{t} = \psi (w_{r}r_{t} + w_{\eta}\eta_{t-1} + w_{z}z_{t-1} + b_{\phi})　（6） \)
\( h_{t} = \alpha h_{t-1} + (1 - \alpha)\phi_{t},　　\alpha \in (0,1)　（7） \)

SR-SVモデルの推定対象となるパラメータは\(θ=(𝛽_0, 𝛽_1,𝜙,𝜎^2,𝑤_ℎ,𝑤_𝑟,𝑤_𝜂,𝑤_𝑧,𝑏_𝜑,𝑏_𝑟 )\)であり、 \(θ\)の推定方法として2つの候補があります。1つ目はSR-SVモデルを状態空間モデルという枠組みで見た最尤法です。その際に計算する尤度に関して、例えばSVモデルの場合でも潜在変数が含まれた重積分となり、解析的に評価することが難しいと知られています。[Watanabe] SR-SVモデルの尤度も同様で、式（8）のような重積分で表されます。

\[ p(y_{1},\cdots,y_{T}|\theta) = \int p(y_{1},\cdots,y_{T},z_{1},\cdots,z_{T}|\theta)dz_{1} \times \cdots \times dz_{T}\\ =\int \prod^{T}_{t=1} p(y_{t}|z_{t})・p(z_{1}|\theta) \prod^{T}_{t=2}p(z_{t}|z_{t-1}, \theta)dz_{1}\times \cdots \times dz_{T}　（8） \]

ここで、それぞれ以下の分布

\( y_{t}|z_{t}～N(0, \exp(z_{t})),　z_{1}|\theta～N(\beta_{0},\sigma^{2}), \)
\( z_{t}|z_{t-1}, \theta～N(\beta_{0} + \beta_{1}h_{t} + \phi z_{t-1}, \sigma^{2}) \)

に従うので、式（8）の被積分関数は次のようになり、尤度を直接計算することは難しいことが分かります。

\( p(y_{1},\cdots,y_{T},z_{1},\cdots,z_{T}|\theta) \)
\[ \propto \prod^{T}_{t=1} \frac{1}{\sqrt{e^{z_{t}}}}・\exp \left(- \sum^{T}_{t=1} \frac{y^{2}_{t}}{2e^{z_{t}}} - \frac{(z_{1}-\beta_{0})^{2}+\varSigma^{T}_{t=2}(z_{t}-\beta_{0}-\beta_{1}h_{t}-\phi z_{t-1})^{2}}{2\sigma^{2}} \right)　（9） \]

よって、尤度の最適化以外のパラメータ推定を考える必要があります。そこで2つ目の手法として、マルコフ連鎖モンテカルロ法（MCMC）に基づくcomputer-intensiveな手法を紹介します。

3. マルコフ連鎖モンテカルロ法（MCMC）

本節では、ベイズ統計におけるマルコフ連鎖モンテカルロ法（MCMC）について復習します。ベイズ統計では、事前分布に尤度（観測データ）を掛け合わせることによって、事後分布の更新を行い、逐次的な情報更新が可能という考え方を前提としています。 （ベイズの定理）

\[ p(x|y) = p(y|x) \frac{p(x)}{p(y)}　（10） \]

ベイズ推定、特にMCMCは尤度の不偏推定量等を用いて事後分布のサンプルを生成できるため、今回のように最尤法が難しい場合でも有効です。同じサンプリングシミュレーションの、通常のモンテカルロ法とMCMCの違いを以下にまとめました。

図表1：通常のモンテカルロ法とMCMCの比較

観点 通常のモンテカルロ法
サンプリングの方法 独立したサンプルを直接母集団から生成
収束性・実装の複雑さ 収束の評価が容易で、基本的な実装のみ（一様サンプリング等）
有効な使いどころ 円周率の近似や、積分領域が単純な場合
観点 MCMC
サンプリングの方法 前のサンプルに依存して連続的なサンプルを提案分布から生成（マルコフ性を利用）
収束性・実装の複雑さ 初期のサンプルを捨てることが必要（バーンイン期間）、提案分布の選択によって効率性が変わる
有効な使いどころ 高次元積分の場合。または複雑な確率分布等、母集団から直接サンプリングが不可な場合

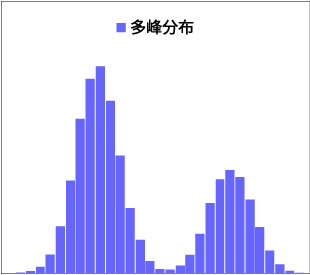
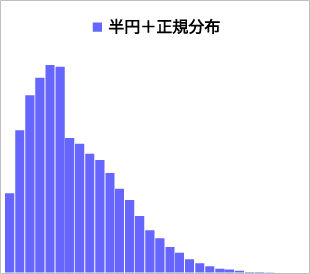
図表2は、MCMCの1つであるメトロポリス法を用いて複雑な分布を生成したものです。MCMCによって多峰性を持つ分布や、半円と正規分布を貼り合わせたような分布といった任意の分布を自在に生成することが可能です。メトロポリス法の詳細のアルゴリズムについては[Hanada]等をご参照ください。

図表2：メトロポリス法による複雑な分布の生成

次節では、MCMCを用いたベイズ的手法によって、 SR-SVモデルのパラメータを推定していきます。

MCMCを用いたSR-SVモデルのパラメータ推定

4. SR-SVモデルのパラメータ推定

実際に、SR-SVモデルのパラメータをベイズ推定（MCMC）によって計算していきます。パラメータの値を返す最尤法（点推定）と異なり、ベイズ推定ではパラメータの事後確率分布を返すため、事前分布を設定する必要があります。ここでは、[Nguyen]と同じ事前分布を仮定します。

\[ \begin{cases} \ \beta_0, w_h, w_r, b_\phi, b_r ～ N(0.0, 0.1)\\ \ \beta_1, w_z ～ IG(2.5, 1.0)\\ \ \sigma^2 ～ IG(2.5, 0.25)\\ \ \dfrac {\phi + 1}{2} ～ Beta(20.0, 1.5)　　（11） \end{cases} \]

ただし、\(N\)(∙,∙)は正規分布、\(IG\)(∙,∙)は逆ガンマ分布、 \(Beta\)(∙,∙)はベータ分布とします。以下の（図表3） は、MCMCによってサンプリングを行った事後分布です。（他パラメータは割愛）補足ですが、サンプリング手法はメトロポリス法(メトロポリス・ヘイスティングス法)をベースにして、提案分布は適応的多変量正規分布と呼ばれるものを仮定しています。

事後分布とMCMCの収束

図表3：SR-SVモデルのパラメータ事後分布（一部）

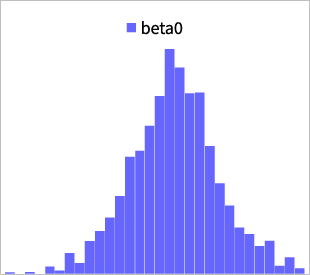
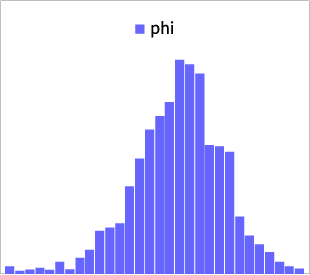
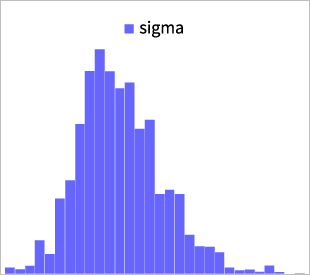
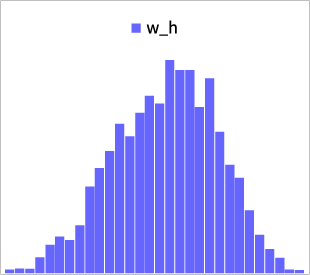
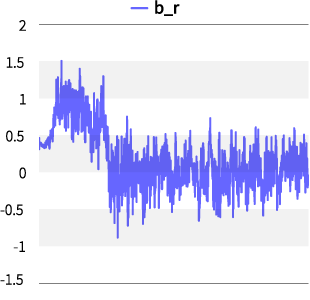
式（11）は共役事前分布なので、事後分布も同じ分布族になることが知られていますが、その様子も確認できました。一般的に、MCMCのサンプリングが上手くいったかどうかは、収束診断や自己相関の確認を行うのが厳密ですが、以下の（図表4）のように乱数の推移で概ね確認することも可能です。 これはトレースプロットと呼ばれ、毛虫のようになっているとMCMCが上手く収束していると言われています。（他パラメータは割愛）

図表4：SR-SVモデルのトレースプロット（一部）

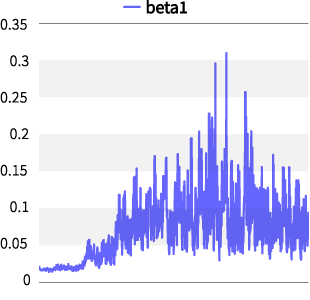
まとめ

5.まとめ

マルコフ連鎖モンテカルロ法（MCMC）はSR-SVモデルの複雑な事後分布（混合・裾の厚い分布含む）を扱うことができ、確率解析におけるマルコフ性（エルゴード性）によって理論的正しさも保証されます。一方、長期のシミュレーションや多変量になると計算時間が長くなり、実務の立場から考えると効率的な実装が求められます。今回割愛しましたが、[Tran]によるブロック化されたサンプリング手法も有名です。その他に、粒子フィルタや変分推論等の代替手法もあり、厳密さと現実的な時間とのトレードオフ関係を見極めることが重要です。

参考文献

  • [Watanabe] 渡部敏明,ボラティリティ変動モデル,朝倉書店,（2000）
  • [Hanada] 花田政範,他,ゼロからできるMCMC マルコフ連鎖モンテカルロ法の実践的入門,講談社（2020）
  • [Nguyen] T.-N. Nguyen,他,A Statistical Recurrent Stochastic Volatility Model for Stock Markets,（2022）
  • [Tran] M.-N. Tran,他,The Block Pseudo-Marginal Sampler,（2017）

クオンツトピックス一覧へ

「クオンツトピックス」ご利用にあたっての留意点

当資料は、市場環境に関する情報の提供を目的として、ニッセイアセットマネジメントが作成したものであり、特定の有価証券等の勧誘を目的とするものではありません。

【当資料に関する留意点】

  • 当資料は、信頼できると考えられる情報に基づいて作成しておりますが、情報の正確性、完全性を保証するものではありません。
  • 当資料のグラフ・数値等はあくまでも過去の実績であり、将来の投資収益を示唆あるいは保証するものではありません。また税金・手数料等を考慮しておりませんので、実質的な投資成果を示すものではありません。
  • 当資料のいかなる内容も、将来の市場環境の変動等を保証するものではありません。
  • 手数料や報酬等の種類ごとの金額及びその合計額については、具体的な商品を勧誘するものではないので、表示することができません。
  • 投資する有価証券の価格の変動等により損失を生じるおそれがあります。