吉野貴晶のクオンツトピックス

No.24
ICと的中率の関係

2024年01月05日号

投資工学開発部
吉野 貴晶

金融情報誌「日経ヴェリタス」アナリストランキングのクオンツ部門で16年連続で1位を獲得。ビックデータやAI（人工知能）を使った運用モデルの開発から、身の回りの意外なデータを使った経済や株価予測まで、幅広く計量手法を駆使した分析や予測を行う。

投資工学開発部
片山 幸成

ニッセイアセット入社後、デリバティブ取引やファンドのリスク管理業務に従事。18年1月より投資工学開発室にて主に機械学習を含む定量的手法、オルタナティブデータを活用した新たな投資戦略の研究開発を担当。

ICが高いファクターはどのくらいの確率で予想が当たるのか考えてみよう

  • IC：情報係数、 Information Coefficient
  • 2次元正規分布

0. 予備知識、keywords

基本的な確率、統計学の知識を仮定します。

キーワード
IC、情報係数、相関係数、正規分布、マクローリン展開

1. Introduction

大学生の時に、ジャッジメンタル運用をされている方が、『上がると予想した銘柄であっても全ての株式が上がるわけではない。投資は51勝49敗の積み重ねです。』という話をされていました。今回は的中率とICの関係性を深掘りしてみたいと思います。
クオンツ運用では、ファクターの有効性を評価する際、一般的にIC（Information Coefficient）を用います。ICはファクタースコアとリターンの相関係数であり（本レポートでは積率相関係数とします）、ファクタースコアが高い銘柄ほどリターンも高く、逆に低いスコアの銘柄ほどリターンが低い傾向がある場合、ICの値は高くなります。
ICの計算には、対象となる銘柄全てにスコアが付与され、魅力的な銘柄ほど高いスコアが与えられるという前提があります。しかしながら、株価が上昇すると予測した銘柄を購入（下落すると予測した銘柄を売却）するというスタイルの投資家にとっては、スコアの付与自体が難しいという問題も存在します。そのため、的中率（株価の上昇・下落予想が当たる）という指標の方が使いやすいでしょう。
以下、ファクタースコアとリターンは正規分布していると仮定します。また、生データではなく平均0、標準偏差1になるように加工している、つまり両者とも標準正規分布に従っていることを仮定します。

2. 用語の定義、整理

ファクタースコアとは、あるファクター（ROE、PBRなど）で見た時の銘柄の魅力度です。PBRの場合は低いと割安感があるので、逆数のBPRを使用し、数値が高いほど魅力的であるように設定します。前述の通り、ICはファクタースコアとリターンの相関係数を指します。ICが高いファクターは有効性が高いと言えます。

的中率は、ファクタースコアが正かつリターンが正、またはファクタースコアが負かつリターンが負となる確率とします。つまり、魅力的だと判定された銘柄が上昇し、魅力的でないと判定された銘柄が下落する確率です。ただし、ファクタースコアまたはリターンが0のケースは考えないものとします（連続的な確率密度関数を仮定しているので、ピッタリ0になる確率自体が0％）。

アークサインの近似

3.　数学的な定式化

的中率とICの関係性を考察してみましょう。IC＝0つまりファクターの予測力が全くない状況では上がるか下がるかはランダムであるため的中率は50％となるはずです。また、ICが高くなると的中率も上がり、IC=1つまり完璧な予測力を持つときは的中率＝100％となっているはずです。

今、\((x,y)\)を（ファクタースコア、リターン）とすると、2次元平面上で、\((x,y)\)が右上（第一象限）または左下（第三象限）にいる確率が的中率であると解釈できます。また、ファクタースコア、リターンはIntoroductionで仮定したように標準正規分布です。考えているファクターのICを\(r\)とします。さらに\((x,y)\)が相関係数\(r\)の2次元正規分布に従っていると仮定しましょう。ここで相関係数\(r\)の2次元正規分布の確率密度関数\(f(x,y)\)は

\[\displaystyle f(x,y) = \frac{1}{2\pi\sqrt{1-r^2}} exp \left( \frac{-1}{2(1-r^2)} (x^2 - 2rxy + y^2) \right) \]

と表すことができます。対称性から第一象限での積分と第三象限での積分は等しいので、今回は第一象限での積分を考えることにします。つまり、\(x,y\)が0～∞の範囲で積分した結果を2倍します。
途中計算は省きますが次の結果になることが知られています。（[RIMS]参照。導出するにはまず\(y=rx+z*\sqrt{(1-r^2)} \)として\(x,z\)での積分問題にした後に、極座標変換をします。その際に傾きが\(-r÷ \sqrt{(1-r^2)}\) の直線が作る三角形を考えると、三平方の定理より斜辺は\(\sqrt{(1-r^2)}\) ですので、直線のなす角度\(\theta\)に対する\(\sin \theta\)は\(-r\)であることが分かり、\(\theta\)の範囲は\(-\arcsin(r)\)から\(π/2\)であることに注意して順次積分計算を行えば計算ができます。）

\[\displaystyle 2 \int_0^{\infty} \int_0^{\infty} f(x,y)dxdy = 2 \left( \frac{1}{4} + \frac{1}{2\pi}\arcsin (r) \right) ･･･（1） \]

ここで\(\arcsin\)は逆正弦関数です。\(\arcsin\)は手計算するのが難しいため簡単に計算できるようにマクローリン展開を用いて、近似することにします。

\[\displaystyle \arcsin(r) = r + \frac{r^3}{6} + \frac{3r^5}{40} + ･･･,\hspace{10pt}-1 < r < 1 \]

\(r\)はICのことでしたが例えば\(r=0.3\)だとしても、三番目の要素は\(3*(0.3)^5 /40 =0.00018225\)であるため、非常に小さい数で計算結果にほとんど影響がないことが分かります。
以下では（1）式で\(\arcsin\)を\(r\)で近似した場合、\(r+r^3/6\)で近似した場合の2通りで調べてみます。

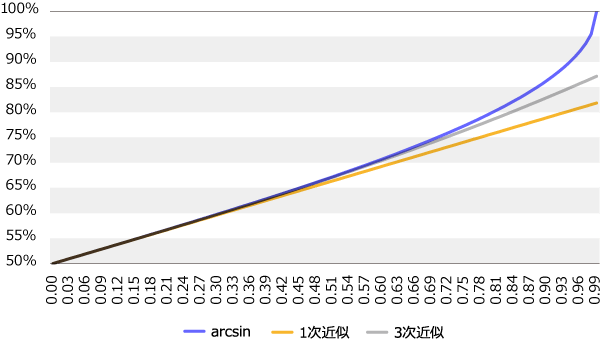
\[\displaystyle 的中率 ≒ 2\left( \frac{1}{4} + \frac{1}{2\pi}r \right) \]あるいは \[\displaystyle 的中率≒2 \left( \frac{1}{4} + \frac{1}{2\pi}(r + \frac{r^3}{6}) \right) \]

（1）に各々代入すると上記の近似式が得られます。ICの水準毎に上記の式に当てはめて計算したものが次のグラフです（横軸がIC、縦軸が的中率）。

図1：アークサインの近似

まとめ

4. 結果の解釈とまとめ

数式の再掲

\[\displaystyle 2 \int_0^{\infty} \int_0^{\infty} f(x,y)dxdy = 2 \left( \frac{1}{4} + \frac{1}{2\pi}\arcsin (r) \right) ･･･（1） \] \[\displaystyle 的中率 ≒ 2\left( \frac{1}{4} + \frac{1}{2\pi}r \right) \]あるいは \[\displaystyle 的中率≒2 \left( \frac{1}{4} + \frac{1}{2\pi}(r + \frac{r^3}{6}) \right) \]

水色のグラフが積分計算で得られた\(\arcsin\)をそのまま用いて計算した数値です。
オレンジ色のグラフは1次近似で、\(\arcsin\)を\(r\)で近似した場合です。
グレーのグラフは3次近似で、\(\arcsin\)を\(r+r^3/6\)で近似した場合です。

ICが1に近い場合は（グラフの右端）グラフが離れていますが、ICが0.3以下の場合、グラフ同士がほとんど重なっているので、1次近似でも3次近似でも高い精度で近似されていることがわかります。実現可能なICの水準を考えると1次近似でも十分でしょう。

有効性が高い目安として使われるIC=0.1の水準であっても的中率は約53%なので、購入した銘柄の大半が上昇するというのは非常に難しいことがわかります。ちなみに的中率が51％となるICは約0.03です。

参考文献

吉野貴晶のクオンツトピックス一覧へ

「吉野貴晶のクオンツトピックス」ご利用にあたっての留意点

当資料は、市場環境に関する情報の提供を目的として、ニッセイアセットマネジメントが作成したものであり、特定の有価証券等の勧誘を目的とするものではありません。

【当資料に関する留意点】

  • 当資料は、信頼できると考えられる情報に基づいて作成しておりますが、情報の正確性、完全性を保証するものではありません。
  • 当資料のグラフ・数値等はあくまでも過去の実績であり、将来の投資収益を示唆あるいは保証するものではありません。また税金・手数料等を考慮しておりませんので、実質的な投資成果を示すものではありません。
  • 当資料のいかなる内容も、将来の市場環境の変動等を保証するものではありません。
  • 手数料や報酬等の種類ごとの金額及びその合計額については、具体的な商品を勧誘するものではないので、表示することができません。
  • 投資する有価証券の価格の変動等により損失を生じるおそれがあります。