No.23
位相空間論入門と抽象的アプローチ

位相空間論に触れてみよう、ヘロンの公式がなぜ存在するのか考えてみよう

0. 予備知識、keywords

高校数学における三角比、ベクトルの知識を仮定します。

キーワード

位相、公理主義、完備性、距離、内積、ノルム

1. Introduction

今回のレポートで取り扱う位相空間に関連する諸概念や数学的な思考方法、アプローチについて説明・考察します。

図1

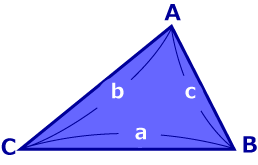
三角形の面積の公式

三角形の面積の公式と言えば、中学時代に習う

\[面積＝底辺×高さ÷2\]

ですが、高校の三角比ではこれを一般化した以下の公式を習います。

\[面積=\frac{1}{2} × ab \sin \angle{C}\]

さらに発展的な内容として、塾や参考書などで、以下のヘロンの公式というものを習った方もいるかと思います。

\[面積= \{s(s-a)(s-b)(s-c) \} ^{ \frac {1}{2}} \]

ここで

\[s= \frac{(a+b+c)}{2}\]

証明は代入して整理するだけなので、省略します。三角形の面積公式は他にもベクトルの成分表示を用いた公式なども知られていますが、他にはないのでしょうか？また、どうしてこのような公式に気付けたりするのでしょうか？
この問いに関して私見を述べる前に位相空間の話に移ります。

2. 位相空間論を学習する理由と学習方法

機械学習等を学んでいると、しばしば位相空間に関連する用語が出てきます。例えば、位相、内積、ノルム、開集合、ヒルベルト空間などです。これらの概念や定理を完璧に理解する必要が実務上あるとは思いませんが、一方で一切知らずどういうものかすら分かっていないと肝心の参考書や論文等を読む上で支障が出てくるでしょう。今回は簡単にこれらの概念について解説します。
位相は現代数学において最も重要な概念の一つであり、数学の専門書を開けば必ず使われると言っても過言ではない必須項目です。しかしながら、位相空間の議論は抽象度が高く数学を専攻する学生ですら挫折する人もいます。また、例えば[Saito]などの本を最初から最後まで把握している人は数学科でも多くはないでしょう。完璧に理解するというよりは話についていける程度に学び、困った時は[Saito]や[Matsuzaka]等を参照するという形で（数学科ですら）十分だと思います。実務家の場合は完璧に理解する必要もありませんし、大学の授業を聴講して学習する必要もありません。昨今ではYoutube等に解説動画があるほか、大学教員の方が講義資料をHPにアップロードしていることも多いため、まずはそれらで一通り基本事項を学ばれるのがよいと思います。なお、単発の資料や動画よりもシリーズものになっている方が学習しやすい印象です。

公理主義

3. シンプルな抽象化と公理主義的抽象化

本レポートでは解説を容易にするため2種類の抽象化を区別して述べます。なお、この用語は一般的な表現ではないので、予めお含み置きください。

シンプルな抽象化

シンプルな抽象化とは、例えば平面ベクトルで考えた問題を3次元空間で考える2次方程式で解の公式がありますが、3次や4次方程式でも同様の解の公式がないかを調べてみる、あるいは、\(x\)という1変数関数について調べていたものを\(x,y\)の2変数関数に拡張してみる、を指すことにします。シンプルな抽象化と言っても簡単に解けるという意味ではないのですが、やりたいことやシチュエーション自体は容易に理解できるでしょう。

一方、公理主義的抽象化は次のようなアプローチを指すことにします。

公理主義的抽象化

関数がベクトルになるという話を聞いたことがある方は多いと思いますが、いわゆる抽象ベクトル空間について解説します。高校数学で習う平面ベクトルについて考えると、\((0,0)\)はどのベクトルに足しても変わらないことや、実数\(k\)に対してベクトルの各成分を\(k\)倍することで、ベクトルのスカラー倍を計算できること、また、このスカラー倍については、ベクトルの加法との間に分配法則が成り立つことが自明です。ベクトル\(u,v\)、スカラー\(k\)に対してベクトルの和\(u+v\)を計算してから、それを\(k\)倍しても、先にスカラー倍して\(ku,kv\)を計算して、その後足しても同じ結果になるという性質も簡単に確認できます。

逆に“これらの性質を満たすものをベクトルと定義”します。

つまり、流れとしては、直感的な意味でのベクトルと呼ばれるものを調べる→ベクトルの性質の中で本質的なものは何かを考える→逆にその性質を満たすものをベクトルと呼ぶ。

これを本レポートでは公理主義的抽象化と呼ぶことにします。関数がベクトルになるというのは、矢印や方向といった一般的な意味でのベクトルではなく、ベクトル関数同士の和やスカラー倍等を適切に定義することによって、上記の公理主義的抽象化ベクトルの性質を満たすようにすることができるという意味です。

このあたりの議論や感覚は文科系の方ですと、哲学的な文脈、例えば、ウィトゲンシュタインの論理哲学論考から考えたほうが分かりやすいかもしれません。論理哲学論考自体が難しい本ですが、例えば[OH]など素晴らしい解説本があります。なお、同じ発音の功利主義という言葉とは全くの別物です。

さて、上述の観点から素朴に考えると、ベクトルではない関数が（公理主義的抽象化によって）ベクトルとみなされること自体に問題があり、適切な定義ではないと感じるかもしれません。一方で、きちんとメリットも存在し、例えば、抽象ベクトル空間において、公理となる条件（性質）のみから様々な定理を導くことができたとします。この場合、一般的な意味でのベクトルであろうが、関数をベクトルとみなしたものであろうが、当然その定理は成立するので議論を流用することができ、個別に具体的な証明が必要とならないため便利です。また、ベクトルという概念がなんとなくこういうものという形ではなく、数学的に定義されているため議論をする上でも認識相違が発生しにくくなり有用です。

この公理主義的抽象化は何もベクトルに限った話ではなく、高校数学で習う内積という概念も位相空間論においては抽象的な形で定義されます。

位相空間論

4. 位相空間論における重要概念

位相は距離を抽象化した概念です。距離は定義から言って数値的に表せるので比較しやすく分かりやすいというメリットがありますが、二つの対象の距離を妥当な形で定義するのが難しいケースもあります。例えば自分を中心とした人間関係を考えた際に、親友は知人より近い印象ですが、数値で各々距離を具体的に示せと言われても困るでしょう。
もう少し曖昧な近さ、あるいは同じ集団に属するといった素朴な感覚を数学的に定義したものが位相で、イメージとしては同じ開集合に属する元同士が近く、空集合と全体集合のみで開集合系になっている時、密着位相とは、すべての元が同じ開集合に集まっている、つまり全部近いので密着しているというイメージです。離散位相とは、その逆に一点集合がすべて開集合系に含まれる、つまり自分と近いものは自分自身しかないので、離れている感が出ているというわけです。

ある空間が完備であるとは、任意のコーシー列が収束列になることを言いますが、分かりやすく言えば、収束先がその空間にちゃんと含まれるイメージです。
例えば、有理数全体の集合は完備ではありません。例としてネイピア数が無理数であることを認めて、数列\(a(n)=(1+ \frac{1}{n})^n \)を考えます。任意の自然数\(n\)について\(a(n)\)は有理数ですが、仮定よりネイピア数は無理数なので、収束先が有理数ではありません。他の反例として\(\sqrt{2}\)に収束する数列であったり、関連する話題として連分数展開等を考えてもよいでしょう。

内積とノルムについては定義通りです。よく知られているように内積からノルムが誘導でき、またノルムから距離を誘導でき、距離から位相を誘導できます。つまり、

学習上の注意点として、しばしば選択公理が証明に必要かどうか精緻な議論をしている参考書等もありますが、強い興味関心がない限り深入りせずに選択公理は使ってよいものと考えて読み進めたほうが早く学習できます。

なお、自然言語処理では多様体を用いた学習方法なども存在しますが、多様体の参考書としては[Matsumoto]が予備知識をあまり必要とせず非常に読みやすいためオススメです。

なぜヘロンの公式が存在するのか

5. なぜヘロンの公式は存在するのか？

最初の問いに戻りましょう。ヘロンの公式はなぜ存在するのか？また、他に三角形の面積公式はないのか、考えてみましょう。

三角形には中学校で習ったように合同条件というものがあります。

合同というのは（厳密な定義はともかく）形がピッタリ同じということなので、面積も当然同じです。
また、逆は真ならずで、面積が同じでも形が違う三角形は無限に存在するので、合同性（形がピッタリと同じこと）は等積性（面積が等しいこと）より、真に強い条件です。つまり合同条件というのは面積を決定するための十分条件ということです。厳密に言えば、「面積が決まること」と「公式という形で表現できること」は異なりますが、三角形のような基本的な図形においては面積の決定条件を用いて公式という形で表現できると考えるのが自然でしょう。

さて、三角比で良く習う公式

もちろん、式変形能力が非常に高く、\(\frac{1}{2} × ab \sin{\angle{C}}\)という公式を見てヘロンの公式が想像できる人もいるでしょうが、上記のような、強い条件（合同性）から弱い条件（等積性）が導かれるという抽象的、普遍的な議論、アプローチを知ることで、各合同条件に対応する面積公式があるのではないか？と想像を働かせることができるのです。

参考文献

• [Heron]
• [Saito]
• [Matsuzaka]
• [Matsumoto]
• [OH]